- годографа метод
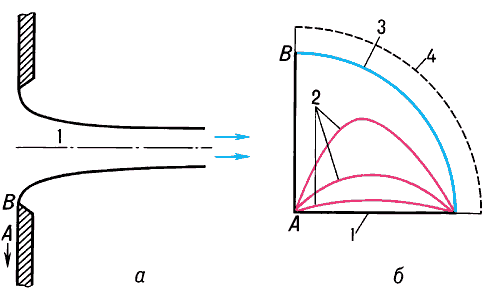
Истечение струи в свободное пространство и соответствующая картина в плоскости годографа.
годо́графа ме́тод (от греч. hodós — путь, движение, направление и grápho — пишу) в аэродинамике — метод исследования и расчёта плоских безвихревых течений сжимаемого газа, основанный на том, что система уравнений для потенциала скорости φ и функции тока ψ, нелинейная в физической плоскости (x, y), становится линейной при переходе к плоскости переменных (u, v) — плоскости годографа скорости (здесь u, v — проекции вектора скорости на оси x, y прямоугольной системы координат). Это возможно ввиду того, что коэффициент исходных уравнений зависят лишь от скорости. Основы метода, использующего преобразование в плоскость годографа, даны С. А. Чаплыгиным в 1902. Система линейных уравнений для φ и ψ преобразуется к каноническому виду (Л. С. Лейбензон, 1935):
 ;
;  ,
,
где ;
;  ;
;  ;
;  ;
;  ;
;а* — критическая скорость; γ — показатель адиабаты.
Представление течения уравнениями в плоскости годографа особенно удобно в задачах с относительно простыми граничными условиями. Такие условия имеют место для течений, на границах которых либо направление скорости, либо её модуль сохраняют постоянное значение; это позволяет сразу построить область течения в плоскости годографа. К этому классу задач относится, например, задача об истечении газовой струи (см. рис.), для которой точное решение уравнений в плоскости годографа строится в виде ряда по совокупности частных решений, найденных методом разделения переменных.
Однако в общем случае расчёт обтекания тел связан с принципиальными трудностями, поскольку точные граничные условия в плоскости годографа неизвестны. В связи с этим широко применяется следующий приближённый метод: в канонических уравнениях коэффициент K принимается равным единице, что выполняется с той или иной степенью точности для произвольного газа при скоростях, не слишком близких к скорости звука, и строго — для так называемого газа Чаплыгина (газа с линейной связью между давлением и удельным объёмом, то есть с γ = ‑1). В результате эти уравнения приводятся к так называемым уравнениям Коши—Римана для действительной и мнимой частей аналитической функции комплексного переменного. На основе такого подхода с помощью метода конформных преобразований удаётся решить задачу о циркуляции обтекании профиля дозвуковым потоком газа. Кроме того, разработан ряд приближённых методов учёта влияния сжимаемости газа на распределение давления по профилю в дозвуковом потоке, не требующих полного решения задачи, а использующих данные о распределении давления в потоке несжимаемой жидкости (методы С. А. Христиановича, Кармана—Тзяна и др.). Они позволяют вводить поправку на сжимаемость в несколько более широких диапазонах углов атаки, относительных толщин профиля и Маха чисел, чем линейная Прандтля—Глауэрта теория.
При околозвуковом обтекании тонкого профиля линейные уравнения в плоскости годографа дополнительно упрощаются в рамках теории малых возмущений и сводятся к так называемому уравнению Трикоми (итальянский математик, F. Tricomi), которое описывает течение с местными сверхзвуковыми зонами.
Литература:
Чаплыгин С. А., Собрание сочинений, т. 2, М.—Л., 1948;
Гудерлей К. Г., Теория околозвуковых течений, пер. с нем., М., 1980;
Седов Л. И., Плоские задачи гидродинамики и аэродинамики, 3 изд., М., 1980;
Лойцянский Л. Г., Механика жидкости и газа, 6 изд., М., 1987.В. Н. Голубкин.
Энциклопедия «Авиация». - М.: Большая Российская Энциклопедия. Свищёв Г. Г.. 1998.
