- сверхзвуковое течение
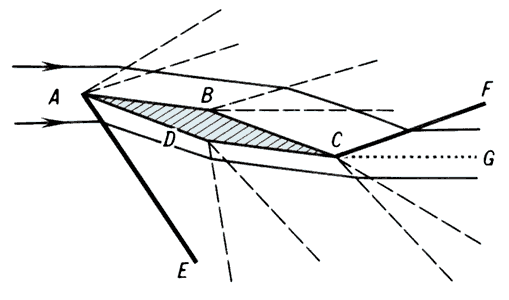
Рис. 1. Сверхзвуковое обтекание ромбовидного профиля.
сверхзвуково́е тече́ние — течение газа, скорость которого в каждой точке рассматриваемой области превышает скорость звука в этой точке, то есть местное Маха число больше единицы (М > 1). На практике С. т. имеет место при движении скоростных самолётов, артиллерийских снарядов, ракет, космических аппаратов, при работе реактивных двигателей, турбин, аэродинамических труб. В общем случае С. т. может быть нестационарным, а газ вязким и теплопроводным. Однако специфические свойства С. т. обычно рассматриваются на примере стационарного движения идеального газа. Малые возмущения физических величин распространяются по частицам газа со скоростью звука, поэтому в С. т. не передаются вперёд, а сносятся вниз по потоку, не выходя из области, находящейся внутри Маха конуса или (в условиях неоднородного потока) внутри более сложной характеристической поверхности (коноида).
При адиабатическом движении газа в сверхзвуковой трубке тока его поведение прямо противоположно случаю дозвукового потока. В С. т. при расширении трубки тока скорость газа увеличивается, а при сужении — уменьшается. Это вызвано тем, что при М > 1 рост (или падение) скорости вдоль трубки тока происходит менее интенсивно, чем соответствующее падение (или рост) плотности газа. Такой эффект используется для получения С. т. в Лаваля сопле. Другое специфическое свойство С. т. — возможность образования в нём ударных волн, или скачков уплотнения, представляющих собой тонкие слои (приближённо принимаемые за поверхности разрыва), при переходе через которые параметры потока изменяются скачкообразно. Ударные волны, в которых происходят необратимые термодинамические процессы с возрастанием энтропии, являются источником волнового сопротивления. В С. т. могут также возникать слабые разрывы гидродинамические, при переходе через которые испытывают скачок не сами газодинамические функции, а лишь их производные. При больших сверхзвуковых скоростях (гиперзвуковое течение) и температурах в газе протекают различные равновесные или неравновесные физико-химические превращения (возбуждение внутренних степеней свободы молекул, диссоциация, ионизация, излучение). Эти реального газа эффекты могут существенно влиять на параметры С. т.
Основной проблемой при рассмотрении С. т. в аэродинамике летательных аппаратов является определение сил, моментов и тепловых потоков, действующих на летательный аппарат и отдельные его элементы (см. Аэродинамические силы и моменты, Аэродинамическое нагревание). К задаче внешнего обтекания примыкают задачи о внутреннем С. т. в диффузорах и соплах, об истечении сверхзвуковой струи, о взаимодействии ударных волн между собой и с препятствиями. Эти проблемы исследуются как экспериментальными, так и теоретическими методами.
С. т. невязкого нетеплопроводного газа описывается квазилинейной гиперболической системой газодинамических уравнений в частных производных. Точные аналитические решения этой системы получены лишь в простейших случаях (сверхзвук, обтекание клина, Прандтля—Майера течение, сверхзвуковой источник). Комбинируя такие решения или используя теорию характеристик и скачков уплотнения, можно аналитически рассчитать и другие виды С. т., например, течение около заострённого профиля и Буземана биплана, плоскую струю. При осесимметричном сверхзвуковом обтекании конуса (см. Осесимметричное течение) система уравнений сводится к двум обыкновенным дифференциальным уравнениям первого порядка, которые легко интегрируются численно. Для тонких тел, когда возмущения сверхзвукового потока малы, можно линеаризовать газодинамические уравнения и развить линеаризованную теорию С. т., дающую довольно простые, но ограниченные по применимости решения. При гиперзвуковых и трансзвуковых скоростях такая линеаризация недопустима, но и здесь возможно использование методов возмущений теории и применение методов построения сращиваемых асимптотических разложений по малым параметрам (см., например, Трансзвуковое течение). Пример аналитически рассчитываемого плоскопараллельного С. т. около ромбовидного профиля в равномерном невозмущенном потоке при отличном от нуля угле атаки дан на рис. 1. От передней и задней точек тела исходят косые скачки уплотнения АЕ и CF. При обтекании выпуклого угла в каждой точке А, В, С, D излома профиля возникает волна разрежения (течение Прандтля—Майера) и происходит разворот линий тока в области, ограниченной линиями Маха (штриховые линии). Остальные участки линий тока прямолинейны. От задней точки C идёт тангенциальный разрыв CG, по обе стороны которого скорости различны, а давление одинаково.
Картина сверхзвукового обтекания под углом атаки затупленного тела вращения значительно сложнее, особенно при наличии у тела изломов образующей. Случай, когда течение имеет плоскость симметрии, показан на рис. 2. За отошедшей головной ударной волной (жирная линия) перед затуплением имеет место смешанное течение с дозвуковой областью (M < 1), которая отсутствует у заостренного тела с углом раствора острия, не превышающим предельного значения для данного числа Маха. Далее за ограничивающей дозвуковую область звуковой поверхностью (M = 1 — пунктир на рисунке) находится область трехмерного вихревого С. т. Здесь, между телом и ударной волной происходит многократное отражение волн разрежения (штриховые линии) и волн сжатия (сплошные линии), причем внутри поля течения возможно образование вторичных ударных волн. На область С. т. влияет поток на предшествующей носовой части тела, который, напротив не зависит от этого С. т. Несравненно сложнее картина С. т. около конфигураций моделирующих целый летательный аппарат. Здесь в поле течения могут иметь место несколько локальных дозвуковых зон.
Расчеты С. т. в общем случае (в частности с учетом высокотемпературных явлений в газе) проводятся численными методами на ЭВМ. Для этой цели применяются различные схемы конечноразностного метода сеток, характеристик метод, метод интегральных соотношений. Вычислительные алгоритмы позволяют эффективно с высокой, нужной для практики точностью рассчитывать С. т. и детально исследовать его структуру. С помощью аналитических и численных методов решаются также различные задачи оптимизации аэродинамической формы тела при С. т., например определение профиля крыла наименьшего сопротивления или формы сверхзвукового сопла с максимальной тягой при заданных ограничениях на их размеры и массу. Для ряда тел, моделирующих элементы летательного аппарата (острые конусы, затупленные клинья и конусы, тела вращения, треугольные крылья, сопла Лаваля), при различных параметрах невозмущенного потока рассчитаны таблицы основных газодинамических функций в поле С. т. Проводятся также численные расчёты сверхзвукового обтекания конфигурации летательного аппарата в целом.
Литература:
Курант Р., Фридрихс К., Сверхзвуковое течение и ударные волны, пер. с англ., М., 1950;
Кочин Е. Е., Кибель И. А., Розе Н. В., Теоретическая гидромеханика, 4 изд., ч. 2, М., 1963;
Ферри А., Аэродинамика сверхзвуковых течений, пер. с англ., М., 1963;
Овсянников Л. В., Лекции по основам газовой динамики, М., 1981;
Черный Г. Г., Газовая динамика, М., 1988.Я. И. Чушкин.
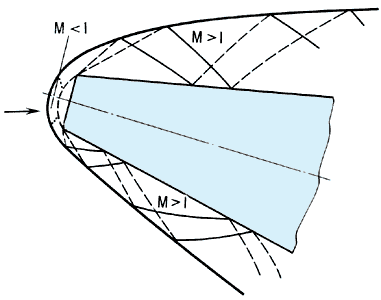
Рис. 2. Сверхзвуковое обтекание затупленного конуса.
Энциклопедия «Авиация». - М.: Большая Российская Энциклопедия. Свищёв Г. Г.. 1998.
