аэродинамическое нагревание

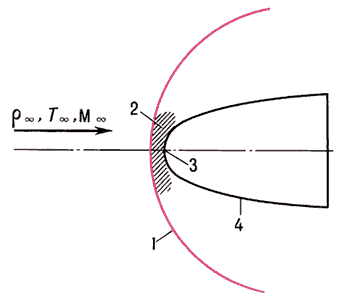
Рис. 1. Схема обтекания затупленного тела сверхзвуковым потоком газа.

аэродинами́ческое нагрева́ние — повышение температуры поверхности летательного аппарата при его полёте в атмосфере. Частицы газа при их движении относительно летательного аппарата тормозятся около его поверхности в зонах сжатия при отклонении потока, в ударных волнах и в пограничных слоях. Процесс торможения сопровождается выделением теплоты за счёт преобразования кинетической энергии поступательного движения частиц в тепловую и, следовательно, повышением температуры газа. При этом могут быть достигнуты значения температуры, близкие к значениям температуры торможения Т₀ в совершенном газе
,

где T_∞, V_∞, M_∞ — температура, скорость и Маха число набегающего потока, c_p — удельная теплоёмкость при постоянном давлении, γ — показатель адиабаты.

А. н. определяется процессами теплообмена между нагретым газом и поверхностью, протекающими в пограничном слое. Задачей расчёта А. н. является определение удельных конвективных тепловых потоков q_ω к поверхности и затем (из уравнений теплового баланса) её температуры T_ω. Если поверхность обтекаемого тела теплоизолирована (имеется теплообмен только с обтекающим газом, q_ω = 0), то она может нагреться до так называемой адиабатической температуры T_r = T_e + rV_e²/2c_p = T_e + r (T₀ – T_e), где Т_е, V_e — температура и скорость потока на внешней границе пограничного слоя, определяемые из аэродинамического расчёта, r — коэффициент восстановления температуры, немного меньший единицы и зависящий от характера течения в пограничном слое.

Температура теплоизолирующей поверхности при М_∞ > 2 достигает значений, которые затрудняют применение алюминиевых сплавов; при М_∞ > 5 стальные конструкции должны иметь тепловую защиту (см. Горячая конструкция, Охлаждаемая конструкция). При M_∞ = 10, наряду с применением охлаждения, использованием жаростойких материалов, приходится допускать также частичный унос материала поверхности (см. Абляция).

В условиях сложного теплообмена А. н. определяется из уравнения локального баланса: q_ω = q₁ + q₂, где q₁ — удельный тепловой поток, передаваемый от поверхности внутрь конструкции (существенно зависит от конструкции летательного аппарата и определяется из расчёта внутренней теплоотдачи), q₂ = εσ(T_ω⁴-T_∞⁴) — удельный радиационный тепловой поток. (ε — так называемая степень черноты поверхности, σ — постоянная Стефана—Больцмана). Конвективный удельный тепловой поток q_ω от газа к поверхности, обусловливающий А. н., принимается пропорциональным разности температур T_r и T_ω: q_ω = α(T_r-T_ω), где коэффициент теплоотдачи α определяется процессами, протекающими в пограничном слое. Поэтому расчёт конвективного теплообмена сводится к расчёту характеристик пограничного слоя, который может быть проведён при заданном распределении параметров течения на его границе.

Формулы для расчёта конвективного теплообмена представляются в виде зависимостей Нуссельта числа Nu и коэффициента r от определяющих подобия критериев и безразмерных пространственных координат x_i/L (i = 1, 2, 3; L — характерный линейный размер, например, хорда крыла): Nu = f₁,(Re, M, T_ω/T_r, Pr, Eu, x_i/L), r = f₂(Re, М, Рr, Eu, x₁/L). Здесь Re — Рейнольдса число, T_ω/T_r — температурный фактор, Eu — число Эйлера, Pr — Прандтля число. Вид функций f₁ и f₂ меняется при переходе ламинарного течения в турбулентное при достижении критического значения числа Рейнольдса Re_*.

Т. о., расчёт конвективного теплообмена может быть сделан после расчёта течения идеальной жидкости; он включает определение значений Re_*, Nu, r. Значение Re_* определяется экспериментально и находится в пределах от 0,6·10⁶ до 0,6·10⁷. Расчёты показывают, что при ламинарном режиме течения r≈Рr^0,5 в (для воздуха r = 0,84), при турбулентном режиме течения экспериментально получено r≈0,88—0,89. Для ламинарного пограничного слоя зависимость для определения теплообмена приводится к виду Nu/(Re)^1/2 = Ф₁Prⁿ, где n = 0,3—0,4, и, следовательно, удельный тепловой поток

(ρe, μ_e — плотность и динамическая вязкость на внешней границе слоя); таким образом, q_w ~ L^‑1/2. Для турбулентного пограничного слоя из экспериментов следует, что при Re < 10⁸ Nu/Re^0,8 = Ф₂Рr^0,43, а удельный тепловой поток
,

то есть q_w~L^‑0,2. Точные значения функции Ф₁, могут быть получены численным интегрированием дифференциальных уравнений пограничного слоя. Для определения функции Ф₂ обычно используются экспериментальные данные.

Исследования показывают, что наибольших значений А. н. достигает в областях повышенного давления в окрестности точек (критических точек) и линий растекания в носовой части тел, на передних кромках крыльев, килей, органов управления и на других выступающих элементах конструкции (рис. 1). При этом для ламинарного режима обтекания тепловые потоки максимальны непосредственно в критических точках, а для турбулентного режима они достигают наибольших значений на участках поверхности, на которых значения плотности потока течения ρ_eV_e максимальны; для двумерного течения это имеет место при числах Маха у поверхности, близких к единице. Коэффициент теплообмена на боковых поверхностях тел значительно меньше, чем в критических точках, однако в связи с большой площадью этих поверхностей тепловая защита требует значительного увеличения веса конструкции. При образовании на поверхности тел шероховатости тепловые потоки могут возрасти из-за более раннего перехода к турбулентному режиму, а также вследствие интенсификации турбулентных тепловых потоков на шероховатой поверхности (в 1,5—2 раза).

Большое значение имеет расчёт А. н. поверхностей гиперзвуковых летательных аппаратов, обладающих подъёмной силой и имеющих органы управления. В этом случае возникают пространственные течения, сопровождающиеся искривлением линий тока и поперечными градиентами давления (рис. 2). Характерной особенностью пограничного слоя при этом является образование вторичных течений, за счёт которых пограничный слой в окрестности линий растекания утончается и тепловые потоки возрастают. Около рулей, щитков, а также при приближении к линиям отекания возможно образование местных отрывных зон с последующим возрастанием теплоотдачи в местах прилипания оторвавшихся потоков (рис. 3).

При M_∞ > 10 температура заторможенного газа достигает значений, при которых становится существенной диссоциация воздуха. Часть кинетической энергии внешнего потока, затраченной на диссоциацию, преобразуется в теплоту в результате рекомбинации у стенки. Большое значение при этом имеют диффузия диссоциированных молекул к стенке и химические реакции, протекающие на поверхности и в пограничном слое. Выражение для расчёта тепловых потоков в химически реагирующей смеси записывается в виде q_w = α (H_r = H_w), где H_r = h_e + rV_e²/2, , . Здесь α = α/с_p — обобщённый коэффициент теплопередачи; H_w — полная энтальпия газа на поверхности, h_ei — энтальпия i-го компонента газа на внешней границе пограничного слоя, с_pi и с_еi — соответственно удельная теплоёмкость при постоянном давлении и концентрация этого компонента, h_xi — теплота образования i-гo компонента смеси, n — число компонентов. Значение α зависит от состава газа и от степени равновесности химических реакций. При ламинарном режиме течения производится интегрирование уравнений пограничного слоя, включающих уравнения диффузии и энергии, учитывающие расход веществ и выделение теплоты при химических реакциях.

При скорости полёта более 10—12 км/с (межконтинентальные ракеты, космические аппараты при входе в атмосферу и др.) в расчёте А. н. необходимо учитывать передачу теплоты к поверхности от разогретого газа за ударными волнами и в пограничном слое за счёт радиационных тепловых потоков. Лучистые тепловые потоки при определенных условиях (толстый ударный слой перед затупленным телом, неравновесная диссоциация) могут сравниться и превысить конвективные тепловые потоки. При температурах, сопровождающих такие полёты, возникает также термическая ионизация воздуха, сильно влияющая на коэффициент конвективного и лучистого переноса.

В связи с появившимися реальными возможностями длительного полёта в верхних слоях атмосферы на высоте более 60—80 км возникла необходимость расчёта А. н. в разреженном газе, когда средний путь свободного пробега молекул сравним с размерами тела или с толщиной пограничного слоя и существенно проявляется дискретность среды (см. Разреженных газов динамика). Из-за малой плотности газа тепловые потоки в этой области течений малы, хотя при скоростях полёта, равных 6—8 км/с, температуры торможении достаточно велики. В этих условиях вся область течений в зависимости от значений параметров подобия Re и М может быть условно разделена на области сплошной среды, течения со скольжением и свободномолекулярного течения. В области течения со скольжением разрежённость среды проявляется в первую очередь у стенки, где скорость и температура газа отличаются от скорости и температуры самой стенки. При свободномолекулярном течении можно пренебрегать числом столкновений молекул между собой по сравнению с числом их столкновений с поверхностью тела.

Для расчёта теплообмена в разреженном газе решающее значение имеет определение коэффициентов аккомодации, характеризующих взаимодействие молекул газа с поверхностями тела. Значения коэффициент аккомодации зависят от загрязнённости поверхностей, их шероховатости, наличия адсорбированной газовой плёнки, соотношения масс молекул газа набегающего потока и атомов материала поверхности и др. При больших скоростях полёта принимают приближенно, что коэффициент аккомодации примерно равен единице.

При полёте на высотах более 100 км роль А. н. уменьшается и, начиная с высот 180—200 км, тепловые потоки за счёт А. н. становятся пренебрежимо малыми по сравнению с лучистыми потоками от Земли и Солнца.

В. С. Авдуевский.

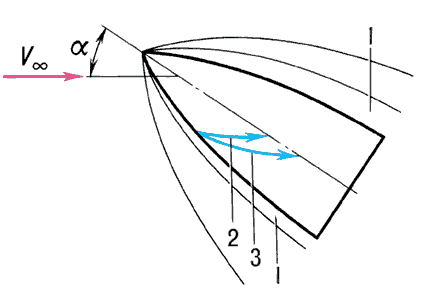
Рис. 2. Обтекание тела под углом атаки сверхзвуковым потоком газа.

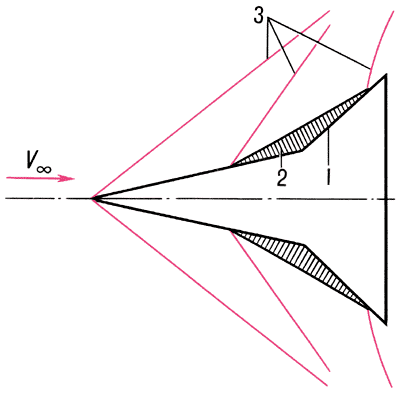
Рис. 3. Схема обтекания тела сверхзвуковым потоком газа.