разреженных газов динамика

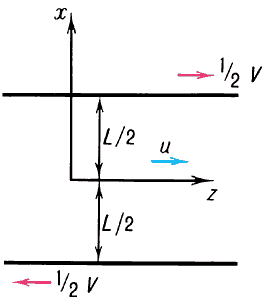
Течение Куэтта.

разреже́нных га́зов дина́мика, раздел газовой динамики, изучающий явления, требующие учёта молекулярной структуры газа и, следовательно, привлечения представлений и методов кинетической теории газов.

Классическая газовая динамика справедлива когда Кнудсена число Kn  1, то есть параметры газа слабо меняются на длине свободного пробега молекул (сплошная среда). Благодаря столкновениям молекул в окрестности каждой точки поля течения устанавливается близкое к равновесному распределение молекул по скоростям, которое определяется несколькими макроскопическими величинами (скоростью течения u, плотностью ρ, температурой T) и производными от них. Это позволяет локальные связи между тензором напряжений, вектором потока энергии и другими величинами, с одной стороны, и газодинамическими переменными u, ρ, Т и их производными — с другой, и построить замкнутую систему газодинамических уравнений. По мере роста числа Kn функция распределения определяется всё большей областью течения, так что невозможно установить локальные связи и получить замкнутую систему уравнений для конечного числа макроскопических величин. Такие течения требуют описания на молекулярном уровне с помощью функции распределения f(v, r, t), удовлетворяющей Больцмана уравнению. Особенности таких течений в наибольшей мере проявляются в предельном случае Kn→∞, когда столкновениями молекул можно пренебречь, так что функция распределения не меняется вдоль потока молекул. Такие течения называются свободномолекулярными течениями. Характер течения определяется столкновениями молекул с ограничивающими течение поверхностями, законами взаимодействия молекул с твердым телом или жидкостью. Свободномолекулярные течения существенно отличаются от течений сплошной среды. Особенно нагляден гипертермический режим, когда скорость набегающего на тело потока много больше тепловой скорости молекул массы m, так что можно считать, что все молекулы движутся с одинаковой скоростью V. Если n — число молекул в единице объёма набегающего потока и S — площадь миделя обтекаемого тела, то число молекул, падающих на тело, равно nVS, а приносимый ими импульс X_i = ρV²S, где ρ = mn. Полное же сопротивление аэродинамическое X = X_i + X_r, где X_r — реактивный импульс отражённых от тела молекул. Если пренебречь импульсом отраженных молекул, то коэффициент лобового сопротивления (см. Аэродинамические коэффициенты) c_xa = X/(½ρV²S) = 2 независимо от формы тела; с учётом X, имеем c_xa > 2. В континуальном режиме (сплошная среда) c_xa хорошо обтекаемых тел составляет десятые или сотые доли единицы, а плохо обтекаемых близок к 1. В гипертермическом потоке подъёмная сила обусловлена лишь реактивным импульсом отраженных молекул. В условиях орбитального полёта скорость отраженных молекул много меньше скорости набегающего потока и коэффициент подъёмной силы c_ya мал. Соответственно аэродинамическое качество K = c_ya/c_xa мало́ независимо от формы обтекаемого тела, в то время как при Kn  1 для крыльев значение K может достигать единиц или десятков. При Kn  1 наибольшая температура тел и газа равна температуре торможения, в то время как в гипертермическом потоке температура теплоизолированного тела выше температуры торможения. Таким образом, характер течения при Kn  1 и Kn  1 существенно различен. Между этими предельными случаями лежит переходный, в котором не пригодны как континуальное описание, так и упрощения свободномолекулярного режима. Здесь приходится решать полное уравнение Больцмана, которое много сложнее Навье—Стокса уравнений. Для его решения наибольшее распространение получил метод статистического моделирования (так называемый метод Монте-Карло). Для получения приближенных решений используются также модельные кинетические уравнения с упрощённым интегралом столкновения. Промежуточная область граничит с областью течения со скольжением, в которой справедливы уравнения Навье—Стокса со скольжения условиями и условиями температурного скачка.

Влияние числа Кнудсена на структуру потока наиболее наглядно прослеживается на примере течения Куэтта — течения, возникающего между двумя параллельными пластинами, расположенными на расстояние L друг от друга, имеющими одинаковую температуру и движущимися в противоположные стороны с постоянными скоростями ±V/2. Если V мала по сравнению с тепловой скоростью молекул, то приближенное решение уравнения Больцмана имеет вид

, ,

где u — скорость газа, τ_xy — постоянное в пространстве между пластинами напряжение трения, μ — динамическая вязкость, c — константа. При Kn  1 газ между пластинами покоится, а напряжение трения пропорционально давлению, так как μ ~ ραλ, где α — скорость звука, λ — средняя длина свободного пробега молекул. При этом проскальзывание u_τ = ½V – u газа относительно стенки максимально и равно V/2. По мере уменьшения числа Kn скольжение уменьшается, и при Kn  1 u = cKnV/2 в соответствии с условиями скольжения для уравнений газовой динамики. Напряжение трения при этом становится пропорциональным μ и градиенту скорости, как это и следует из континуальной газовой динамики. В течении Куэтта характеристики монотонно изменяются с изменением Kn. Однако в других течениях многие характеристики в промежуточной области значений Kn не монотонны. Так, при течении по трубе объёмный расход имеет минимум при некотором значении Kn (парадокс Кнудсена). Не монотонны и аэродинамические характеристики. Например, сопротивление тонких тел (пластина, параллельная потоку, конус) имеет максимум. При обтекании таких тел в результате межмолекулярных столкновений на тело попадают молекулы, которые, не будь столкновений, пролетели бы мимо тела, что и приводит к увеличению сопротивления по сравнению с сопротивлением в случае свободномолекулярного течения.

Сложность решения уравнения Больцмана и отсутствие во многих случаях надёжных данных о взаимодействии молекул между собой и поверхностями делают актуальным эксперимент. Для исследования течений разреженного газа используются <<вакуумные аэродинамические трубы, а взаимодействие молекул с поверхностями изучается с помощью молекулярных пучков. При создании вакуумных труб возникают сложные проблемы моделирования течений, так как законы взаимодействия молекул между собой и поверхностями существенно зависят от температур газа и стенки, так что для полного моделирования недостаточно выдержать натурные значения <<Маха числа M и <<Рейнольдса числа Re, но необходимо выдержать и натурные значения температур газа и тела. Для этого приходится нагревать газ в форкамере и охлаждать модель. Как правило, удаётся достичь лишь частичного моделирования. Вакуумные трубы позволяют исследовать многие детали континуальных течений. Разреженность газа (увеличение λ) позволяет «растянуть» течение. Так, например, ударную волну или кнудсеновский слой, имеющие при нормальных условиях толщину порядка 10^‑7 м, можно растянуть до размеров, приемлемых для исследования их структуры. Для экспериментального изучения течений разреженного газа, наряду с очень чувствительными весами, датчиками давления и потоков теплоты, используются электронные, рентгеновские, лазерные (основанные на флуоресценции и рассеянии) методы диагностики.

Важным объектом исследований являются струи, истекающие в вакуум или в область с низким давлением. Такие струи широко применяются для управления космическими и воздушно-космическими аппаратами, а также характерны при работе вакуумных аэродинамических труб. В струях течение может проходить все режимы — от течений, характерных для сплошной среды, до свободномолекулярного течения, в них происходят релаксационные процессы, химические реакции, конденсация и образование кластеров (твёрдых частиц или капель жидкости). Поэтому струи являются удобным объектом для изучения этих процессов, определения констант реакций, времён релаксации и т. д. Поскольку разные газы в струях ведут себя по-разному, то в них можно получить разделение газов и изотопов, а также выделение различных веществ в виде кластеров. Методы Р. г. д. используются при исследовании течений в пористых телах и капиллярах, для исследования движения и испарения дисперсных сред.

Литература:
Коган М. Н., Динамика разреженного газа. Кинетическая теория, М., 1967; Кошмаров Ю. А., Рыжов Ю. А., Свирщевский С. Б., Экспериментальные методы в механике разреженного газа, М., 1981;
Берд Г., Молекулярная газовая динамика, пер. с англ., М., 1981;
Белоцерковский О. М., Численное моделирование в механике сплошных сред, М., 1984.

М. Н. Коган.