- вязкой жидкости течение
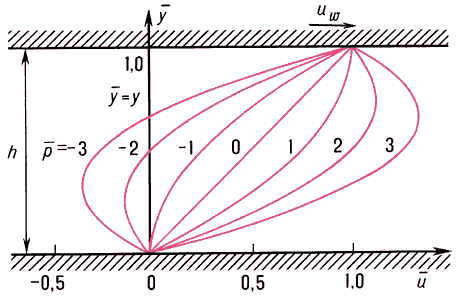
Рис. 1. Распределение скоростей жидкости в течении Куэтта.
вя́зкой жи́дкости тече́ние — движение сплошной изотропной среды, в которой возникают как нормальные, так и касательные напряжения. В. ж. т. происходит под действием сил двух видов: массовых сил, которые пропорциональны массе частицы и в аэро- и гидродинамических задачах являются заданными величинами, и поверхностных сил, которые возникают в результате взаимодействия соседних объёмов жидкости и характеризуются вектором напряжений pn (индекс обозначает направление нормали к площадке, к которой приложена поверхностная сила) Значение pn зависит от ориентации площадки. Из анализа равновесия сил и моментов, действующих на элементарный объём жидкости, следует, что напряжённое состояние жидкости в рассматриваемой точке поля течения определяется симметричным тензором напряжения. В аэро- и гидродинамике вектор pn обычно представляют в виде pn = ‑p + τn, где p — давление гидродинамическое, которое действует по нормали к площадке и значение которого не зависит от ориентации площадки, τn — вектор вязких напряжений, значение которого обращается в нуль в идеальной жидкости и который характеризуется тензором вязких напряжений ||T|| = (τij), i, j = x, y, z — декартовы координаты.
В отличие от твёрдого тела при движении жидкости её частицы перемещаются относительно друг друга. В данный момент времени поле скоростей в малой окрестности рассматриваемой точки есть наложение трех движений: однородного поступательного движения со скоростью V; вращения как твердого тела с угловой скоростью ω/2, где ω = rotV — вектор вихря или завихренности частицы жидкости, чисто деформационного движения, которое определяет отличие движения частицы жидкости от движения твердого тела и характеризуется тензором скоростей деформаций ||Φ||. Между тензорами ||T|| и ||Φ|| существует определенная связь, которая называется реологическим уравнением жидкости. В аэро- и гидродинамике обычно рассматриваются так называемые ньютоновские жидкости с линейным реологическим уравнением (обобщённый закон Ньютона) ||Т|| = λdivV + μ||Φ||, которое представляет собой главные члены реальной связи при бесконечно малых возмущениях. Здесь μ — динамическая вязкость, которая характеризует вязкие напряжения, связанные со сдвиговой деформацией жидкости. ξ = λ + 2/3μ — вторая или объёмная вязкость характеризует вязкие напряжения, обусловленные объемным расширением жидкости. Так как для несжимаемой жидкости divV = 0, величина ξ может играть роль только при движении сжимаемой жидкости; в большинстве аэродинамических задач предполагается, что
ξ = 0(λ = ‑2/3μ — гипотеза Стокса).Движение вязкой жидкости описывается системой уравнений, которые выражают сохранения законы и могут быть записаны как в интегральном, так и в дифференциальном виде. Формула их записи зависит от способа исследования движения жидкости — методом Лагранжа или методом Эйлера, Ниже всюду используется эйлерова форма записи уравнений. Эта система уравнений включает в себя неразрывности уравнение, Навье-Стокса уравнения и уравнение энергии. В общем случае она замыкается уравнением состояния движущейся среды и зависимостями термодинамических функций и коэффициент переноса (см. Переносные свойства среды) от давления и температуры (энтальпии), а её решение должно удовлетворять заданным начальным условиям. Наиболее простой вид система уравнений имеет для несжимаемой жидкости:

Где F — вектор массовой силы, ρ — плотность, T — температура, e — внутренняя энергия, k — теплопроводность, t — время, D/Dt — полная производная, Δ — оператор Лапласа, здесь и ниже Ф — диссипативная функция (см. Энергии уравнение). В отличие от движения идеальной жидкости, для которого имеет место обратимости теорема, уравнения динамики вязкой жидкости описывают необратимый процесс. Необратимость процесса движения связана с диссипацией энергии, то есть переходом части механической энергии в теплоту. Это доказывается вычислением работы A сил, приложенных к поверхности элементарного объёма жидкости, для несжимаемой жидкости имеем
 .
.Таким образом, работа, производимая поверхностными и массовыми силами над единицей объёма жидкости в единицу времени, частично идёт на изменение кинетической энергии этого объёма, а другая её часть, равная Ф, соответствует количеству механической энергии, превращающейся из-за действия сил трения в теплоту. Интегрирование Ф по всему пространству, занятому движущейся жидкостью, позволяет определить общие потери энергии в единицу времени. Этот результат можно использовать, например, для расчёта гидродинамического сопротивления тела, движущегося в жидкости, если известно поле скоростей соответствующего течения.
Анализ уравнений динамики вязкой жидкости значительно упрощается для некоторых классов течений, когда в силу их вырожденности и ряда упрощающих предположений задача сводится к решению системы обыкновенных дифференциальных уравнений. Это так называемые точные решения. Наиболее обширный класс точных решений имеет место для несжимаемой жидкости, например, течение Гагена—Пуазёйля (см. Ламинарное течение) течение Куэтта (рис. 1), возникающее при движении в вязкой жидкости одной бесконечной плоскости (верхняя на рис. 1) с постоянной скоростью uω параллельно другой, находящейся на расстоянии h от неё, при наличии градиента давления dp/dx, характеризуемого параметром
 , равным
, равным  = ‑h2(2μuw)(dp/dx). Для этого течения зависимость скорости и жидкости от поперечной координаты у имеет вид:
= ‑h2(2μuw)(dp/dx). Для этого течения зависимость скорости и жидкости от поперечной координаты у имеет вид: =
=  [1 +
[1 +  (1 –
(1 –  )],, где
)],, где  = u / uw,
= u / uw,  = y / h.
= y / h.Для сжимаемой жидкости число. точных решений невелико. Простейшим примером является одномерная задача о переходе потока совершенного газа в отсутствие массовых сил из одного однородного состояния (при x→-∞) в другое однородное состояние (при x→ + ∞), при этом приведенные скорости потока λ1 = u1/a1, при x→-∞ и λ2 = u2/a1, при x→ + ∞ (u1, u2 — скорости потока соответственно при x→-∞ и при x→ + ∞, a1 — критическая скорость звука при x→-∞) связаны соотношением λ1·λ2 = 1. Аналога такому течению для несжимаемой жидкости не существует, а для идеальной сжимаемой жидкости ему соответствует переход сверхзвукового потока в дозвуковой через прямую ударную волну (рис. 2). Полученное решение позволяет оценить толщину ударной волны δ:
δ/l = (λ1 + l)/(λ1-1),
где l — длина свободного пробега молекул. Следовательно, с увеличением скорости набегающего сверхзвукового потока
(λ1→λmax = [(γ + 1)/(γ-1)]1/2, γ — показатель адиабаты) нарушается предположение механики сплошной среды: δ/l >> 1, и для анализа структуры ударной волны необходимо пользоваться уравнениями, описывающими разреженных газов динамику.В общем случае интегрирование уравнений динамики вязкой жидкости представляет собой сложную математическую задачу и может быть проведено только численно. Разработанные методы численного анализа позволяют решать задачу об обтекании тела при таких Рейнольдса числах, когда силы трения и инерции имеют одинаковый порядок во всём поле течения; при этом проведение расчётов сопряжено с очень большими затратами машинного времени. Однако в предельных случаях малых (Re→0) и больших (Re→∞) чисел Рейнольдcа исследование В. ж. т. можно значительно упростить. В первом случае, который соответствует, например, движению сильновязких жидкостей, силы внутреннего трения значительно больше инерционных сил, и в результате соответствующих упрощений приходим к более простым Осеена уравнениям. При больших числах Рейнольдса силы трения в основной части потока пренебрежимо малы и становятся соизмеримыми с инерционными силами лишь в тонком пристеночном (пограничном) слое жидкости. В этом случае задача об обтекании тела потоком вязкой жидкости распадается на две самостоятельные задачи: задачу об обтекании тела потоком идеальной жидкости, описываемую Эйлера уравнениями, и задачу о расчёте течения вязкой жидкости в пограничном слое, описываемую уравнениями Прандтля. Поскольку движение самолётов и других летательных аппаратов происходят, как правило, при больших числах Рейнольдса, то этот подход позволяет успешно решать многие практические вопросы, связанные с расчётом аэродинамических характеристик и аэродинамического нагревания летательного аппарата.
Литература:
Кочин Н. Е., Кибель И. А., Розе Н. В., Теоретическая гидромеханика, 4 изд., т. 1, 2, Л.—М., 1948—63;
Бэтчелор Дж., Введение в динамику жидкости, пер. с англ., М., 1973;
Лойцянский Л. Г., Механика жидкости и газа, 6 изд., М., 1987.В. А. Башкин.
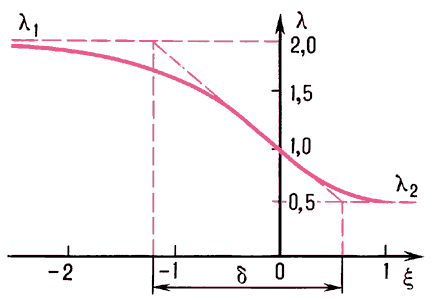
Рис. 2. Изменение приведённой скорости одномерного потока вязкого сжимаемого газа с начальными параметрами.
Энциклопедия «Авиация». - М.: Большая Российская Энциклопедия. Свищёв Г. Г.. 1998.
