- Чаплыгина—Жуковского условие
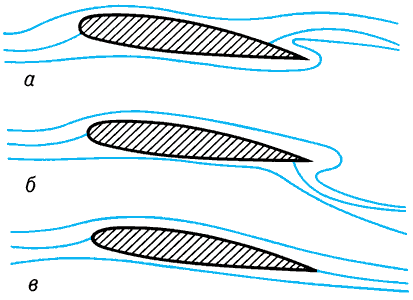
Рис. 1. Схема обтекания гладкого профиля с острой задней кромкой потоком идеальной жидкости.
Чаплы́гина—Жуко́вского усло́вие — требование конечности скорости потока в острой задней кромке гладкого профиля крыла при безотрывном обтекании его потоком идеальной жидкости. Сформулировано С. А. Чаплыгиным и использовано Н. Е. Жуковским для вычисления подъёмной силы профиля в 1910. Одно из основных положений аэродинамики, используемое для определения циркуляции скорости Г вокруг профиля, которое позволило вместе с Жуковского теоремой о подъёмной силе создать крыла теорию в рамках модели идеальной жидкости.
Картина обтекания гладкого профиля с острой задней кромкой потоком идеальной жидкости зависит от значения Г. В случаях а и б на рис. 1 скорости на острой кромке становятся бесконечными, и только в случае в, когда поток сходит с задней кромки, скорости будут иметь конечные значения как в этой точке, так и во всём поле течения. Таким образом, Ч.—Ж. у. позволяет из множества течений выделить единственное, имеющее реальный смысл, и, следовательно, математически однозначно сформулировать задачу обтекания профиля потоком идеальной жидкости. Ч.—Ж. у. носит весьма общий характер и отражает механизм возникновения циркуляции скорости вокруг профиля, связанный с проявлением реальных свойств среды. Например, при обтекании тонкого профиля в начальный момент времени на задней кромке под влиянием сил трения образуется вихрь интенсивности — Г, который затем отрывается н уносится потоком на бесконечность. В результате около профиля устанавливается течение, близкое к потенциальному с циркуляцией скорости Г.
В современной теории крыла Ч.—Ж. у. используется как в классическом варианте, так и в виде различных обобщений. При наличии у профиля нескольких острых кромок (например, у пластины) или ряда точек излома (например, у многоугольника) стационарная постановка задачи приводит к физически нереальным течениям, так как Ч.—Ж. у. можно удовлетворить только в одной из этих точек. Однако успешно развиваются нестационарные подходы, в которых допускается сход вихревых пелен (волнистые линии на рис. 2) со всех острых кромок или изломов, что позволяет применять в них Ч.—Ж. у. и получать всюду конечные скорости. Развитие численных методов сделало возможным переход к ещё более сложным задачам теории крыла, в которых учитываются и вязкие отрывы (неидеальные жидкости). Дополнение модели, основанной на схеме идеальной среды, теорией нестационарного пограничного слоя позволяет проводить расчёт более сложных схем обтекания профиля (рис. 3). У задней кромки Ч.—Ж. у. применяется в обобщённом виде: здесь пограничный слой переходит в вихревой след, который моделируется дискретными вихрями свободными. Кроме того, аналогичные следы образуются и в местах отрыва пограничного слоя.
С. М. Белоцерковский.
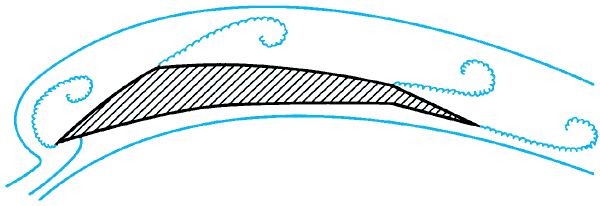
Рис. 2. Схема нестационарного обтекания профиля с острыми кромками и изломами.
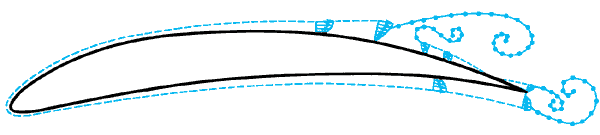
Рис. 3. Схема нестационарного обтекания профиля с отрывами пограничного слоя.
Энциклопедия «Авиация». - М.: Большая Российская Энциклопедия. Свищёв Г. Г.. 1998.
