- Стокса формула
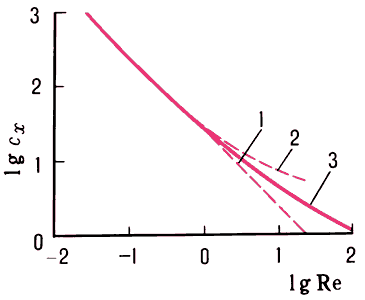
Зависимость cx сферы от Re.
Сто́кса фо́рмула сопротивления сферы — формула, определяющая силу сопротивления X сферы диаметра d, движущейся в покоящейся вязкой несжимаемой жидкости с постоянной скоростью V∞ при малых Рейнольдса числах Re l: X = 3πμdV∞, или в безразмерном виде (см. Аэродинамические коэффициенты):
 ,
,где ρ — плотность жидкости, μ — динамическая вязкость, cx — коэффициент сопротивления. В отличие от известного результата для умеренных и больших чисел Рейнольдса, когда сила сопротивления пропорциональна квадрату скорости, в рассматриваемом случае она зависит от неё линейно; при этом треть силы сопротивления обусловлена силами давления, а две трети — силами трения. Эти формулы установлены Дж. Стоксом (1851) в результате решения линейных уравнений, которые получаются из Навье—Стокса уравнений отбрасыванием в них инерционных членов и называются уравнениями Стокса. Однако уравнения Стокса некорректно описывают течение на больших расстояниях от поверхности сферы, где инерционные силы и силы трения имеют одинаковый порядок. Более корректное во всём поле течения решение задачи можно получить на основе линейных <<Осеена уравнений; приближенное решение задачи в этом случае даёт:
 .
.Сравнение результатов расчётов по приведённым формулам с результатами эксперимента (см. рис.) указывает на их применимость при Re < l.
С. ф. используется при анализе движения мелких сферических частиц в сильно вязких жидкостях, пылевидных частиц и капелек воды в атмосфере и т. п.
В. А. Башкин.
Энциклопедия «Авиация». - М.: Большая Российская Энциклопедия. Свищёв Г. Г.. 1998.
