ламинарный пограничный слой

Рис. 1.

ламина́рный пограни́чный слой — пограничный слой, в котором имеет место ламинарное течение. Поведение Л. п. с. описывается уравнениями Л. Прандтля, решение которых для заданных начальных и граничных условий в общем случае можно получить только численно с помощью ЭВМ, и зависит от ряда определяющих параметров: Рейнольдса числа и Маха числа, формы тела и параметров жидкости или газа. Характерной особенностью математического описания Л. п. с. является возможность преобразования уравнений Прандтля таким образом, что в новых безразмерных переменных преобразованного уравнения не зависят явно от числа Рейнольдса, благодаря этому значительно сокращается объём вычислений при решении практических задач. Кроме того, существуют классы задач, когда в Л. п. с. реализуется автомодельное течение, а решение уравнений Прандтля сводится к интегрированию системы обыкновенного дифференциального уравнения. Их численный анализ проводится достаточно просто, а результаты расчётов позволяют установить и понять основные закономерности развития Л. п. с. и используются для приближённой оценки сопротивления трения и аэродинамического нагревания летательного аппарата.

Практический интерес представляет установившееся движение жидкости или газа в Л. п. с. при нулевом градиенте давления. Для несжимаемой жидкости такое течение реализуется на плоской бесконечно тонкой пластине, помещённой в однородный поток со скоростью V_∞ под нулевым углом атаки; в этом случае скорость потока на внешней границе Л. п. с. u_e = V_∞. После введения функции тока ψ (x, y) и перехода к безразмерным переменным по соотношениям

ψ(x, y) = (2vu_e)^1/2f(η), y = (2vx/u_e)^1/2η

система уравнений Прандтля сводится к обыкновенному дифференциальному уравнению f′′′ + ff′′ = 0 с краевыми условиями f(0) = f'(0) = 0, f′(∞) = 1, где, x, y — оси координат, направленные вдоль и по нормали к поверхности пластины, v — кинематическая вязкость. В этом случае местный коэффициент сопротивления трения определяется выражением

,

где ρ — плотность, Re = u_ex/v — число Рейнольдса, τ_ω — местное напряжение трения (эта задача была решена немецким ученым Г. Блазиусом в 1908, а приведённое уравнение называется его именем). Расчёты для c_f толщин пограничного слоя δ, вытеснения δ* и потери импульса δ** дают: c_f(Re)^1/2 = 0,664; δ(Re)^1/2/x = 5, δ*(Re)^1/2/x = 1,73, δ**(Re)^1/2/x = 0,664. На этом примере видна природа Л. п. с. как области завихренного течения (рис. 1, а, штриховой линией обозначена толщина Л. п. с.): острая кромка пластины при взаимодействии её с набегающим потоком из-за сил трения является источником завихренности. Порождаемая этим источником завихренность путём конвекции и диффузии сносится вниз по потоку и распределяется по некоторой области а окрестности плоской пластины, при этом суммарный поток завихренности через любое поперечное сечение Л. п. с. остаётся постоянным.

Рассмотренная задача допускает обобщение на Л. п. с. при обтекании сжимаемой жидкостью так называемые изотермические пластины. Характеристики Л. п. с. при движении сжимаемой и несжимаемой жидкости в качественном отношении имеют одинаковый характер изменения вдоль поверхности, но отличаются в количественном отношении, и это различие зависит от определяющих параметров задачи. Для совершенного газа ими будут Маха число M_∞ и температурный фактор _ω (отношение температуры стенки T_ω, к температуре T_r, теплоизолирующей поверхности, на которой местный тепловой поток равен нулю). Влияние определяющих параметров на величину c = c_j/(Re)^1/2 показано на рис. 2. Для модели совершенного газа: показатель адиабаты γ = 1,4, Прандтля число Pr = 1,7, динамическая вязкость μ ~ Т^0,76. Анализ задачи позволяет также установить аналогию Рейнольдса, то есть связь между местным Стантона числом St, характеризующим интенсивность местного тёплого потока, и c_j: St = c_j/2S, где S = Pr^2/3 — коэффициент аналогии Рейнольдса. Результаты решения уравнений для плоской пластины в сжимаемом газе непосредственно можно использовать для расчета напряжения трения и теплообмена на поверхности клиньев, обтекаемых сверхзвуковым потоком с присоединённым к вершине скачком уплотнения (см. Ударная волна).

Аналогичная автомодельная задача имеет место для осесимметричного Л. п. с. на поверхности острого кругового конуса, обтекаемого сверхзвуковым потоком под нулевым углом атаки с присоединенным к вершине скачком уплотнения, за которым реализуется коническое течение невязкого газа. Анализ уравнений Прандтля показывает, что при одних и тех же определяющих параметрах задачи характерные толщины Л. п. с. на поверхности конуса в 3^1/2 раз меньше, а местные коэффициенты c_j и St в 3^1/2 раз больше соответствующих величин на плоской пластине. Характерной особенностью поведения Л. п. с. на поверхности рассмотренного класса заострённых тел является обращение c_j и St в бесконечность, а характерных толщин — в нуль на острой передней кромке и вершине. Следовательно, в этих точках на поверхности летательного аппарата при его движении со сверх- и гиперзвуковыми скоростями в плотных слоях атмосферы будут иметь место максимальные тепловые нагрузки.

Другой практически важной задачей является течение жидкости или газа в Л. п. с. в окрестности критической точки затупленного тела (точка на поверхности тела, где скорость невязкого потока обращается в нуль, рис. 1, б). В этом случае скорость потока на внешней границе пограничного слоя пропорциональна продольной координате (u_e∞x), и решение уравнений Прандтля с помощью приведённых преобразований также сводится к интегрированию обыкновенного дифференциального уравнения. Согласно расчётам для плоскопараллельного течения несжимаемой жидкости c_j(Re)^1/2 = 2,46, что намного превышает соответствующее значение для плоской пластины и объясняется влиянием отрицательного градиента давления. Из условия η = const следует, что в окрестности критической точки толщина Л. п. с. принимает постоянное, отличное от нуля, значение. Решение подобной задачи для осесимметричного течения приводит к результату c_j(Re)^1/2 = 2,62. Сравнение с расчётами для плоской задачи показывает, что при наличии отрицательного градиента давления пространственность течение значительно меньше влияет на c_j чем в случае течения при нулевом градиенте давления. Решения аналогичных задач для сжимаемой жидкости показывают, что характеристики Л. п. с. в качественном отношении ведут себя так же, как и при течении несжимаемой жидкости. Таким образом, в окрестности критической точки затупленного тела толщина Л. п. с. имеет постоянное конечное значение, τ_ω∞x, а местный тепловой поток постоянен и ограничен по своему значению. Это важный результат для практических приложений, который означает, что для снижения максимальных тепловых нагрузок сверх- и гиперзвуковые летательные аппараты должны иметь затупленные передние кромки и вершины.

Литература:
См. при статье Пограничный слой.

В. А. Башкин.

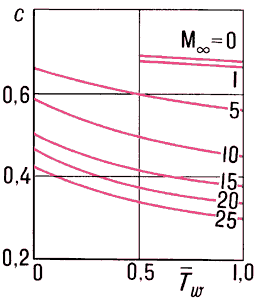
Рис. 2.