- частотная характеристика
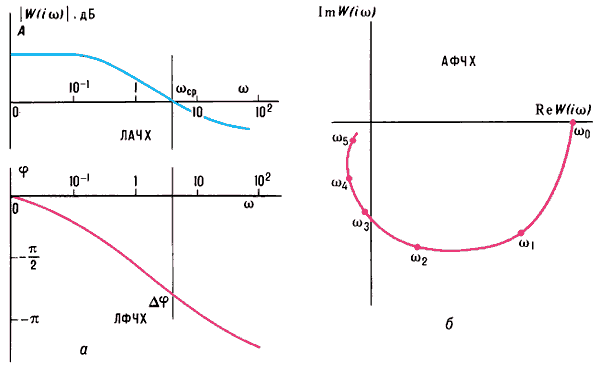
Частотные характеристики разомкнутой системы.
часто́тная характери́стика в теории автоматического регулирования — зависящий от частоты комплексный коэффициент связи между рассматриваемым параметром системы и входным воздействием; Ч. х. существуют, если вынужденная составляющая движения системы является периодической функцией одного периода (одной частоты ω) с периодом вынуждающего воздействия. Если входной сигнал (воздействие) xвх и выходной сигнал (отклик на воздействие) xвых системы представить в комплексном виде:
xвх = Aвх(ω)exp{i[ωt + φвх(ω)]},
xвых = Aвых(ω)exp{i[ωt + φвых(ω)]},
где Aвх(ω), Aвых(ω) — амплитуды, φвх(ω), φвых(ω) — фазы соответственно входного и выходного сигналов, то отношение W(iω) = xвых/xвх системы; при этом величину |W(iω)| = Aвых(ω)/Aвх(ω) называют амплитудно-частотной характеристикой (АЧХ), а величину arga W(iω) = φвых(ω)-φвх(ω) — фазовой частотной характеристикой (ФЧХ). В практике часто используют логарифмические амплитудно-частотные характеристики (ЛАЧХ) и логарифмические фазовые частотные характеристики (ЛФЧХ). При их построении по осям абсцисс откладывают частоту в логарифмическом масштабе, а по осям ординат |W(iω)|, — выраженную в дБ, и φ в линейном масштабе (см. рис., а). При этом частота среза ωср, при которой ЛАЧХ пересекает ось абсцисс, может служить мерой быстродействия системы, а запас по фазе ∆φ(∆φ = π-|φ(ωср)|) — мерой затухания свободных колебаний в ней. Функцию W(iω), построенную на комплексной плоскости в координатах ReW(iω), ImW(iω) (см. рис., б), называют амплитудно-фазовой частотной характеристикой (см. также Годографа метод). Для нелинейных систем за Aвых и φвых принимаются амплитуда и фаза первой гармоники выходного сигнала. В этом случае Ч. х. зависит от амплитуды входного сигнала, а при некоторых сочетаниях параметров системы — и от направления (увеличения или уменьшения, см., например, Гистерезис) изменения частоты. Изложенное выше справедливо для так называемых непрерывных стационарных систем; в более общем случае линейных непрерывных и импульсных систем Ч. х. определяют как отношение комплексных спектров выходного и входного сигналов. У системы, имеющей n параметров состояния и k входных воздействий, насчитывается n·k независимых Ч. х. Например, короткопериодическое продольное движение самолёта характеризуется изменениями угла атаки α и скорости тангажа ωz; самолёт имеет четыре Ч. х. по этим параметрам при отклонении δв руля высоты и воздействии вертикальных порывов ветра со скоростью W, являющиеся функциями iω: α/δв, α/W, ωz/W, а комбинациями этих Ч. х. являются Ч. х. по перегрузке ny: ny/δв, ny/W.
Ч. х. широко используются при анализе системы «самолёт—лётчик—система управления» благодаря возможности определения её динамических характеристик по Ч. х. отдельных элементов, устанавливаемых расчётными или экспериментальными методами. Ч. х. применяются для определения запасов устойчивости замкнутых систем по Ч. х. разомкнутых, для выяснения параметров автоколебаний при наличии в системах нелинейностей и реакции систем на детерминированные и случайные воздействия, для математического моделирования элементов систем по их Ч. х. В общем случае Ч. х. системы связана с её передаточной функцией W(p) соотношением W(iω) = W(p)p = ω.
Широкое использование экспериментальных методов определения Ч. х. привело к созданию и внедрению в исследовательскую практику специализированных приборов — анализаторов Ч. х., включающих генераторы гармонических сигналов, измерительные и вычислительные устройства.
Литература:
Техническая кибернетика. Теория автоматического регулирования, под ред. В. В. Солодовникова, кн. 1—3, М., 1967—69.Ю. Г. Живов.
Энциклопедия «Авиация». - М.: Большая Российская Энциклопедия. Свищёв Г. Г.. 1998.
