турбулентность

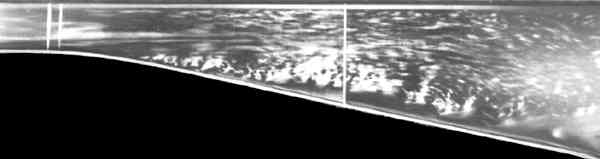
Рис. 1. Течение вблизи стенки диффузора.

турбуле́нтность (от лат. turbulentus — бурный, беспорядочный) — физическое явление, характеризующееся нерегулярными взаимными перемещениями объёмов среды (жидкости или газа) и их перемешиванием и сопровождающееся хаотическими изменениями газодинамических переменных в пространстве и времени. Термин предложен английским физиком У. Томсоном. Важной чертой Т. является сложная вихревая структура течения с широким спектром масштабов движений (размеров вихрей) — см. рис. 1. Исследование Т. — одна из наиболее сложных и важных проблем современной аэро- и гидродинамики.

О. Рейнольдс предложил (1884) для исследования Т. применять статистический подход, при котором конкретные реализации движения среды не рассматриваются, газодинамические переменные (скорость, давление и т. д.) трактуются как случайные величины и используются методы теории вероятностей. Полное статистическое описание Т. возможно лишь с привлечением бесконечного числа так называемых моментов пульсирующих величин — осреднённых их значений и произведений (типа < u_i >, < u_i u_j >, < pu_i > и т. д.) или (что эквивалентно) набором всевозможных плотностей распределения вероятностей (типа P(u₁), Р(u₁, u₂), Р(u, р) и т. д. для любых наборов точек пространства и времени. Первые уравнения для моментов были получены Рейнольдсом (уравнения Рейнольдса и уравнения баланса энергии турбулентности, см. Турбулентное течение) в 1894, а общий метод построения бесконечной цепочки таких уравнений, основанный на использовании Навье—Стокса уравнений, был предложен советский учёными А. А. Фридманом и Л. В. Келлером в 1924. Первые уравнения для плотностей распределения вероятностей были получены А. С. Мокиным, Е. А. Новиковым и В. Р. Кузнецовым в 1967.

Анализ уравнений и экспериментальные исследования статистических характеристик Т. позволили составить ясную в основных чертах картину процессов в турбулентном течении. Кинетическая энергия пульсационного движения (энергия Т.) черпается из осреднённого течения за счет турбулентного трения между слоями среды (хотя возможны локальные области с отрицательной турбулентной вязкостью, где идет обратный процесс) и распространяется по пространству путём конвекции и «диффузии»; перераспределение энергии Т. по направлениям осуществляется за счёт пульсаций давления, а диссипация кинетической энергии пульсаций скорости, то есть переход ее в теплоту, происходит под действием молекулярных напряжений.

При больших турбулентных Рейнольдса числах Re_τ = u′L/ν, где и' — среднеквадратичное значение пульсации скорости, L — интегральный масштаб Т. (характерный размер крупных вихрей, содержащих основную долю кинетической энергии Т.), ν — молекулярная кинематическая вязкость, имеет место так называемая развитая Т., при которой формируется каскадный процесс передачи кинетической энергии от крупномасштабных последовательно ко всё более мелкомасштабным движениям; диссипация кинетической энергии происходит в самых малых вихрях, в которых уже существенно влияние молекулярной вязкости. Этот физический механизм Т. был сформулирован английским учёным Л. Ричардсоном в 1922.

Крупномасштабная Т. характеризуется вихрями, размеры которых соизмеримы с характерным размером осреднённого течения, и определяется конкретной геометрией течения и различными воздействиями на поток — массовыми силами, тепловыделением в химических реакциях и т. п. (при некоторых условиях могут возникать и более крупномасштабные упорядоченные движения — так называемые когерентные структуры). Такая Т. формирует обменные процессы в потоке в целом, осреднённое течение и мгновенные поля газодинамических переменных, приводит к таким важным для приложений явлениям, как пульсации давления на стенках обтекаемых тел и генерации акустического шума. Мелкомасштабные пульсации определяют, например, воздействие атмосферной турбулентности на летательном аппарате, влияют на рассеяние радиолокационных сигналов, на процессы дробления и испарения капель в двухфазных потоках и т. д.

При теоретическом исследовании Т. широко используется модель однородной Т., то есть Т., статистические свойства которой одинаковы во всех точках пространства. Однородная Т. допускает физически наглядное и удобное для теоретических исследований спектральное описание, при котором турбулентное движение представляется в виде суперпозиции гармонических (синусоидальных) колебаний определяющих величин. Модель однородной Т. используется во многих задачах, в которых рассматривается влияние на Т. магнитной, электрической и гравитационной сил, объёмного тепловыделения, распространение волн химических реакций (горения и др.) при наличии Т., влияние деформации среды на Т. (например, в каналах переменного сечения, соплах) и т. д.

Важным частным случаем однородной Т. является изотропная Т., свойства которой в каждой точке не зависят от направления. Понятие изотропной Т. было введено Дж. Тейлором (1935), динамические уравнения получены Т. Карманом и английским учёным Л. Хауартом (1938). Изотропная Т. реализуется в заполненной вихрями безграничной среде с нулевой средней скоростью. Из-за диссипации энергия пульсаций уменьшается со временем по степенному закону (u')²∞t^‑n; из теории следует n = 1, в опытах получают 0,85 < n < 1,6, при этом мелкие вихри затухают быстрее крупных и L увеличивается. Т., близкая по свойствам к изотропной, наблюдается в турбулентных течениях за сетками и решетками, используемыми, в частности, в аэродинамических трубах, а затухание Т. происходит вдоль потока. Рис. 2 иллюстрирует изменение интенсивностей ε Т. вдоль (ε₁) и поперёк (ε₂) потока (ε₁ = u'_i/υ₀, где υ₀ — скорость потока) по тракту дозвуковой аэродинамической трубы. В форкамере 1 Т. затухает, в сопле 2 из-за деформации потока развивается анизотропность Т. (ε₁≠ε₂), в выходном канале 3 происходят изотропизация Т. и уменьшение её энергии.

Согласно представлениям, выдвинутым А. Н. Колмогоровым (1941), изотропная Т. реализуется для произвольной развитой Т. в вихрях малых размеров. Такая мелкомасштабная Т. определяется средней скоростью диссипации энергии, не зависящей в силу каскадного механизма от Re_τ и имеет для всех течений одинаковую структуру, в частности, универсальное распределение энергии Т. по размерам вихрей. В области «инерционного» интервала масштабов вихрей L>>  l>>  η(η ~ LRe^‑3/4 — характерный размер вихрей, в которых происходит основная диссипация энергии Т.) распределение энергии по размерам вихрей l носит степенной характер («закон пяти третей») E(k) = Cε^2/3/k^5/3, где k — волновое число (k ~ 1/l), E(k) — спектр энергии турбулентности, C — постоянная Колмогорова (согласно экспериментальным данным C = 1,8—2,5).

Общая теория Т., задача которой, исходя из уравнений Навье—Стокса, определить статистические характеристики Т. по их начальным данным, ещё не создана. Принципиальная трудность («проблема Т.») связана с незамкнутостью любой конечной системы динамических уравнений — число неизвестных статистических характеристик всегда больше числа уравнений — и необходимостью привлечения бесконечной цепочки уравнений. Для решения прикладных задач разработано большое число полуэмпирических теорий, основанных на уравнениях для тех или иных простейших статистических характеристик Т. (средняя скорость, энергия и масштаб Т., турбулентное трение и т. д.) и использующих дополнительные связи между статистическими величинами, получаемые на основе физических соображений и экспериментальных данных. Попытки построения приближённых методов замыкания динамических уравнений без привлечения эмпирических констант относятся большей частью к изотропной Т. (М. Д. Миллионщиков, 1941; американский учёный Р. Крейчнан, 1969, и др.). Разработанные методы, однако, не являются универсальными и могут приводить к физически неоправданным результатам.

Возможность принципиального прогресса в теории Т. связывается с сочетанием детерминистского подхода для крупномасштабной Т., моделируемой с помощью ЭВМ, и статистического подхода для мелкомасштабной Т. Исследованию квазиупорядоченных крупномасштабных («когерентных») структур Т. уделяется значительное внимание. Полный расчёт конкретных реализации Т. на основе уравнений Навье—Стокса является для реальных ЭВМ проблематичным в практически интересных случаях из-за чрезвычайно широкого диапазона масштабов движений.

Литература:
Бэтчелор Дж. К., Теория однородной турбулентности, пер. с англ., М., 1955;
Хинце И. О., Турбулентность. Ее механизм и теория, пер. с англ., М., 1963;
Монин А. С., Яглом А. М., Статистическая гидромеханика. Механика турбулентности, ч. 1—2, М., 1965—67.

В. Л. Зимонт.

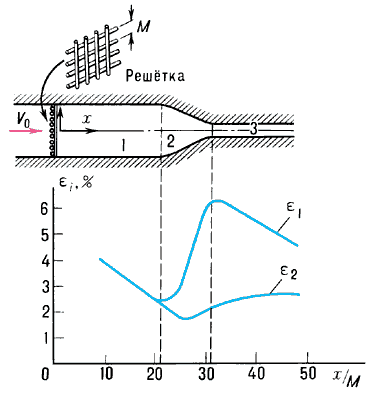
Рис. 2. Интенсивность турбулентности в канале квадратного сечения.