- струйных течений теория
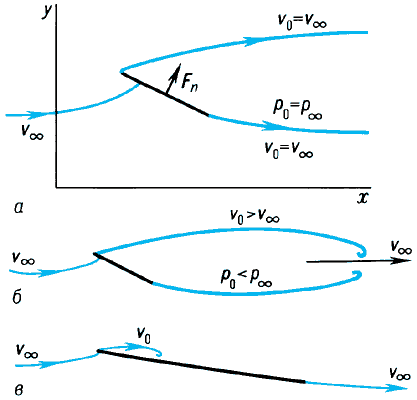
Струйное обтекание пластинки.
стру́йных тече́ний тео́рия — раздел гидродинамики, изучающий течения идеальной жидкости или газа, ограниченные частично твёрдыми стенками и частично свободными поверхностями, на которых давление и, согласно Бернулли уравнению, скорость жидкости постоянны. При этом предполагается, что массовыми силами и поверхностным натяжением можно пренебречь.
Схема струйного течения (СТ) с образованием в жидкости свободных поверхностей тангенциальных разрывов была предложена Г. Гельмгольцем (1868). В 1869 Г. Кирхгоф решил первые задачи плоских потенциальных СТ несжимаемой жидкости, в частности истечения струи из отверстия в стенке и обтекания пластинки под углом атаки α с отрывом потока от её кромок и образованием «застойной» (отрывной) области, давление p0 в которой равно давлению p∞ в набегающем потоке (на «бесконечности», рис., а). При истечении из отверстия С. т. т. позволяет определить форму струи и коэффициент её сжатия. Струйное обтекание пластинки по схеме Кирхгофа, в отличие от сплошного обтекания, при котором тело в потенциальном, потоке не испытывает сопротивления (Д’Аламбера—Эйлера парадокс), дает силу Fn, действующую по нормали к пластинке, и соответственно силу сопротивления Fy = Fnsinα и подъёмную силу Fy = Fncosα. Коэффициент нормальной силы Cn на единицу ширины пластинки выражается формулой Рэлея (1876)
 ,
,где ρ — плотность жидкости, v∞ — скорость потока на бесконечности, l — длина пластинки. Эта сила, равно как получающаяся по формуле Ньютона (см. Ньютона теория обтекания), —
Cn = 2sin2α,
и по формуле, полученной Н. Е. Жуковским для случая безотрывного обтекания пластинки при наличии подсасывающей силы, —
Cn = πsin2α,
(последняя при α > 15° не соответствует экспериментальным данным). Позже были открыты кавитационные течения, возникающие в капельной жидкости с образованием за телом паровых или газовых каверн, в которых давление p0 < p∞. Разрежение в каверне характеризуется числом кавитации σ:
 .
.В отличие от СТ Кирхгофа (σ = 0), кавитационные течения имеют свободные границы конечной длины. Известны различные кавитационные схемы (Жуковского—Рошко, Рябушинского, Эфроса, Ву, Кузнецова и др.), различающиеся способом замыкания каверны. Наиболее совершенной, свободной от «лишних» параметров, является схема Тулина—Терентьева, в которой границы каверны заканчиваются спиралевидными (при математическом описании бесконечнолистными) завитками (рис., б). В реальных отрывных течениях при больших Рейнольдса числах Re давление в отрывных областях вблизи тела практически постоянно, и при правильном выборе σ кавитационного течения оказываются их удовлетворительной расчётной моделью. Для малых углов атаки, когда срыв потока происходит только с передней кромки пластинки, используется схема частичной кавитации (рис., в), оказывающаяся для заданных α и σ двузначной по длине каверны и значению Cn.
Для построения простых СТ применяется годографа метод комплексной скорости
 . В заданной области годографа непосредственно или путём её конформного отображения на более простую определяется комплексный потенциал скорости
. В заданной области годографа непосредственно или путём её конформного отображения на более простую определяется комплексный потенциал скорости  , после чего течение в физической плоскости строится квадратурой:
, после чего течение в физической плоскости строится квадратурой: .
.Более общий приём был предложен Жуковским (1890). Он ввёл функцию
 и производную комплексного потенциала dw/du как функции параметрического переменного и в канонической области (верхней полуплоскости). В случае СТ с кусочно-прямолинейными твёрдыми границами функции ω(u) и dw/du определяются по формуле Шварца—Кристоффеля или методом особых точек (С. А. Чаплыгин), после чего находится
и производную комплексного потенциала dw/du как функции параметрического переменного и в канонической области (верхней полуплоскости). В случае СТ с кусочно-прямолинейными твёрдыми границами функции ω(u) и dw/du определяются по формуле Шварца—Кристоффеля или методом особых точек (С. А. Чаплыгин), после чего находится .
.В случае криволинейных профилей заданной формы построение СТ сводится к решению интегродифференциального уравнения, причём точки схода свободных границ в рамках теории невязкой жидкости находятся из условия, согласно которому кривизна свободной границы в этих точках должна быть равна кривизне твёрдой границы.
Чаплыгину принадлежит обобщение теории плоских СТ на случай потенциальных дозвуковых течений газа. Известны также решения более общих задач теории струй: нестационарного обтекания, течений тяжёлой и капиллярной жидкостей и др. Осесимметричные и пространственные СТ не имеют конечных аналитических решений и изучаются в линейном приближении или численно.
С. т. т. используется для расчёта сил воздействия потока на обтекаемое тело и формы каверн в кавитационных течениях, определения формы струй при их истечении из отверстий, построения каналов, тел и профилей с участками заданной постоянной скорости жидкости или газа, а также в теории отрывных течений вязкой жидкости при больших числах Рейнольдса в качестве модели внешнего потенциального течения, взаимодействующего с пограничным слоем и следом за телом.
Литература:
Биркгоф Г., Сарантонелло Э., Струи, следы и каверны, М., 1964;
Гуревич М. И., Теория струй идеальной жидкости, М., 1979;
Гогиш Л. В., Степанов Г. Ю., Турбулентные отрывные течения, М., 1979.Г. Ю. Степанов.
Энциклопедия «Авиация». - М.: Большая Российская Энциклопедия. Свищёв Г. Г.. 1998.
