криогенная аэродинамическая труба

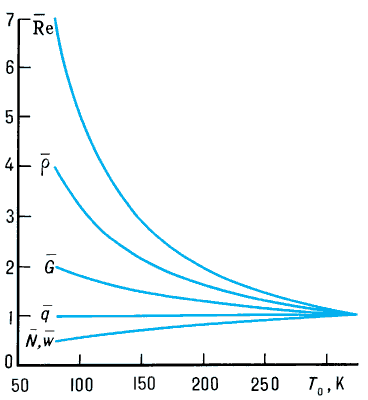
Зависимости относительных значений числа Рейнольдса.

криоге́нная аэродинами́ческая труба́ (от греч. krýos — холод, мороз, лёд и ‑genēs — рождающий, рождённый) — аэродинамическая труба, в которой рабочий газ охлаждается вплоть до температуры начала равновесной конденсации в потоке. Охлаждение потока производится с целью повышения Рейнолъдса числа Re за счёт уменьшения динамической вязкости. Другие известные способы увеличения Re путём увеличения полного давления p₀ или характерных размеров l аэродинамической трубы и модели приводят к увеличению требуемой для проведения эксперимента мощности привода (N∞p₀l²), тогда как увеличение чисел Рейнольдса путём снижения температуры торможения T₀ приводили уменьшению мощности привода (N∞T^0,5).

Охлаждение рабочего газа — воздуха или азота — производится обычно путём впрыска и испарения в нём жидкого азота. При заданных давлении p₀ и размере рабочей части l имеют место следующие зависимости основных параметров К. а. т. от температуры торможения при Маха числе M = const: Re∞T₀^‑1,4, расход газа G∞T₀^‑0,5, скорость ω∞T₀^0,5 и скоростной напор q = ρω²/2∞Gω/2 не зависит от T₀ (см. рис.). При Re = const, p₀ = const расход полной энергии для обычной компрессорной трубы требуется примерно в 2 раза больший, чем для криогенной включая затраты на получение жидкого азота. Постоянство скоростного напора а является очень важным качеством К. а. т.: при охлаждении потока (p₀ = const) Re растёт, а нагрузка на модель не изменяется, что позволяет исследовать раздельно влияние значения Re и аэроупругости на аэродинамические характеристики модели.

При криогенных температурах свойства воздуха (или азота) отличаются от свойств совершенного газа. Однако эти отличия при давлениях до 0,4 МПа и температурах, которые превышают температуры конденсации, составляют не более 1% и практически не сказываются на газодинамических характеристиках потока. Потому при анализе экспериментальных данных и проведении аэродинамических расчётов можно пользоваться уравнениями для совершенного газа с показателем адиабаты γ = 1,4.

А. Л. Искра.