- обратимости теорема
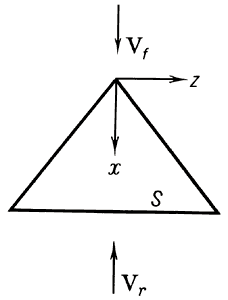
Рис.
обрати́мости теоре́ма в аэродинамике — устанавливает интегральную связь между скосами потока и аэродинамическими нагрузками на тонком крыле при обтекании прямым (Vf) и обращённым (Vr) потоками:
 Пf(x,z)wr(x,z)dxdz =
Пf(x,z)wr(x,z)dxdz =  Пr(x,z)wf(x,z)dxdz
Пr(x,z)wf(x,z)dxdzЗдесь Vf — скорость прямого и Vr(Vr = ‑Vf) — скорость обращённого потоков, П — разность давлений на верхней и нижней поверхностях крыла (аэродинамическая нагрузка) при произвольно заданном распределении скоса ω(x, z) (индекс f относится к прямому потоку, r — к обращённому), интегрирование приводится по поверхности крыла S (см. рис.). Справедлива при обтекании крыла идеальной несжимаемой жидкостью, а также до- и сверхзвуковым потоком газа, когда уравнение для потенциала скорости является линейным в точной постановке задачи или приближённо. Доказывается применением формулы Грина к этому линейному уравнению с учетом соответствующих граничных условий. Приведённая формулировка О. т. сохраняет силу и в случае нестационарного обтекания крыла при гармонических зависимостях функций от времени t, если входящие в неё величины трактовать как амплитуды этих зависимостей, например ω(x, z, t) = ω(x, z)exp(iωt) (ω — частота).
Из О. т. вытекает ряд следствий, которые упрощают расчёт действующих на крыло аэродинамических сил и моментов. Согласно одному из них, подъёмная сила крыла в прямом потоке имеет то же значение, что и в обращённом. При стационарном сверхзвуковом обтекании плоского крыла со стреловидной передней и прямой задней кромками это даёт возможность, переходя к обращённому обтеканию, вычислять коэффициент подъёмной силы крыла конечного размаха по Аккерета формулам, как и для пластины бесконечного размаха.
Другое следствие относится к расчёту аэродинамических сил и моментов крыла с деформирующейся поверхностью или отклоняемыми органами управления. Полагая ωr = 1, получим в левой части приведённого выше равенства подъёмную силу крыла. Если рассчитать распределение давления на жёстком крыле с таким постоянным значением скоса потока в обращенном потоке и воспользоваться О. т., то можно исследовать влияние на подъёмную силу нестационарных деформаций поверхности крыла и отклонения органов управления, выбирая соответствующее распределение скоса ωf и вычисляя интеграл в правой части. Задавая линейные распределения ωr = x или ωr = z, придём к аналогичному результату для продольного момента или момента крена.
О. т. обобщается и на случай произвольного нестационарного обтекания тонкого крыла. Одно из её важных следствий при этом гласит, что импульс подъёмной силы (продольного момента, момента крена), сообщаемый крылу за всё время нестационарного обтекания, совпадает с импульсом, определённым по квазистационарной теории (если значение импульса конечно).
Литература:
См. при статье Нестационарное течение.В. И. Голубкин.
Энциклопедия «Авиация». - М.: Большая Российская Энциклопедия. Свищёв Г. Г.. 1998.
