инерционное взаимодействие

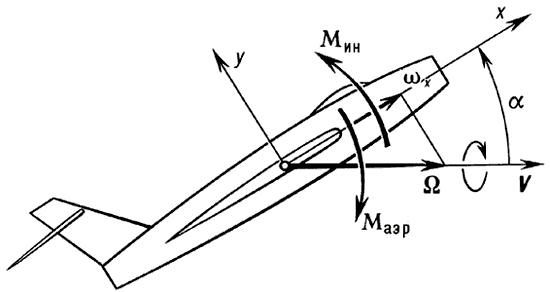
Инерционное взаимодействие продольного и бокового движений самолёта.

инерцио́нное взаимоде́йствие продольного и бокового движений самолёта — проявляется при пространственных манёврах, сопровождающихся энергичным вращением относительно продольной оси. Наиболее значительно И. в. у сверхзвуковых самолётов, имеющих большие различия в значениях главных моментов инерции (вытянутый эллипсоид инерции). С ростом скорости крена И. в. приводит к изменению параметров продольного движения и бокового движения, а также к возникновению влияния продольного управления на рыскание и путевого управления на движение по тангажу. При пространственном движении установившееся вращение самолёта происходит относительно оси, практически совпадающей с вектором скорости полета. Причиной И. в. являются инерционные моменты, действующие на самолёт при его вращении. Эти моменты стремятся опрокинуть самолёт относительно скорости V. На рисунке схематически изображено вращение самолёта и действие инерционного и аэродинамических моментов (предполагается, что скольжение отсутствует). Для малых углов атаки α эти моменты можно считать линейно зависящими от α, так что суммарный момент M_zΣ, действующий на самолёт, можно представить следующим образом: M_zΣ = M_zаэр + M_zин = [m_z^αqSb_A + (I_y-I_x)ω²_x]α, где M_zаэр, M_zин — аэродинамический и инерционный моменты; I_y, I_x — моменты инерции самолёта относительно продольной x и нормальной y осей; S, b_A — площадь и средняя аэродинамическая хорда крыла; m^α_z — производная коэффициент аэродинамического момента тангажа по углу атаки; ω_x — скорость крена; q — скоростной напор. Из условия δM_zΣ/δα = 0 можно оценить критическую скорость крена, при которой происходит потеря устойчивости движения самолёта по тангажу:

Аналогичная оценка получается и для критической скорости крена, при которой происходит потеря устойчивости движения по рысканию:

,
где I_z — момент инерции самолёта относительно поперечной оси z, l — размах крыла, m^β_y — производная коэффициента аэродинамического момента рыскания по углу скольжения. Эти приближённые соотношения не учитывают действия части аэродинамических моментов M_zаэр, обусловленных вращением (так называемых демпфирующих моментов), а также гироскопического момента вращающегося ротора двигателя. Демпфирующие аэродинамические моменты могут существенно изменить критические скорости ω_α, ω_β и даже привести к их исчезновению (см. Аэродинамическое демпфирование). Гироскопический момент изменяет критические скорости незначительно. Скорость крена, при достижении которой самолёт оказывается на границе устойчивости, находится вблизи критических скоростей ω_α, ω_β. При этом в зависимости от типа маневра характер потери устойчивости может носить апериодический или колебательный характер. Особенности пространственного движения самолёта, проявляющиеся в потере устойчивости движения, в возникновении обратной реакции самолёта по перегрузкам на отклонения органов управления, в возможности существования критических режимов инерционного вращения, главным образом порождаются И. в.

Литература:
Бюшгенс Г. С., Студнев Р. В., Динамика пространственного движения самолёта, М., 1967.

М. Г. Гоман.