- Жуковского теорема
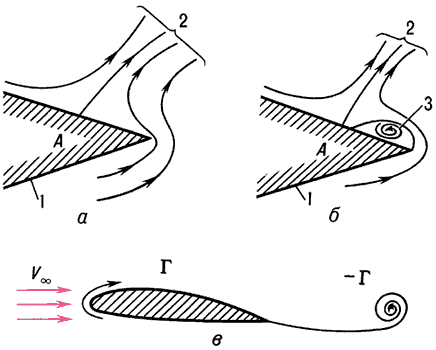
Схемы обтекания задних кромок профиля.
Жуко́вского теоре́ма устанавливает связь между вектором аэродинамической силы, приложенной к профилю, и циркуляцией скорости Γ вокруг него и формулируется так: при безотрывном обтекании произвольного профиля однородным установившимся потенциальным потоком идеальной несжимаемой жидкости его сила сопротивления X = 0, а подъёмная сила вычисляется по формуле
Y = ‑ρ|V∞|Γ,
где ρ — плотность, V∞ — вектор скорости набегающего потока. Была доказана Н. Е. Жуковским (1904) путём применения импульсов теоремы к контрольному контуру, охватывающему профиль.
Значение Ж. т. состоит в том, что она связывает создание подъёмной силы с образованием вихрей в потоке. Но она не даёт ответа на вопросы: как образуются вихри в потоке идеальной жидкости и чему равно значение Γ (неединственность решения задачи). Эти вопросы взаимосвязаны, и ответы на них следует искать в проявлении свойств неидеальности среды — в проявлении сил трения.
Пусть профиль с острой задней кромкой, который обычно применяется в прикладной аэродинамике, начал мгновенно двигаться с постоянной скоростью из состояния покоя (согласно Ж. т. значение подъёмной силы на установившемся режиме не зависит от предыстории движения). В начальный момент движения около профиля устанавливается поле течения, соответствующее потенциальному бесциркуляционному течению идеальной жидкости; при этом положение задней критической точки A в общем случае не совпадает с острой кромкой профиля (см. рис. а). Одновременно под действием сил трения на обтекаемой поверхности начинает развиваться тонкий пограничный слой, который в окрестности задней кромки в области течения с положительным градиентом давления отрывается; в результате с поверхности сходит вихревая пелена, которая сворачивается в вихрь (рис. б), а вихрь сносится набегающим потоком. Сбегающие вихри воздействуют на поле невязкого течения и в конечном счёте видоизменяют его таким образом, что задняя критическая точка смещается на острую кромку. Поскольку движение жидкости в глобальном масштабе является бесциркуляционным, то сход вихрей с острой кромки приводит к образованию циркуляции скорости Γ вокруг профиля, интенсивность которой равна по абсолютному значению и противоположна по знаку интенсивности снесённых на бесконечность вихрей (рис. в). На этом режиме обтекания профиля сводятся к минимуму область отрывного течения и влияние области вязкого течения на внешний невязкий поток. Следовательно, при применении Ж. т. значение Γ должно выбираться из условия равенства нулю (или конечному значению) скорости на острой задней кромке профиля, которое называют Чаплыгина—Жуковского условием. Результаты расчётов подъёмной силы по Ж. т. для таких профилей хорошо согласуются с экспериментальными данными, и с этим связано фундаментальное значение Ж. т. в аэрогидродинамике: на ней базируются теория крыла конечного размаха, теория гребного винта и т. п. Ж. т. была обобщена на случай обтекания решётки профилей.
Из Ж. т. следует справедливость Д’Аламбера—Эйлера парадокса о равенстве нулю аэродинамического сопротивления произвольного профиля, помещённого в однородный поток идеальной жидкости. В реальных условиях все тела обладают конечным сопротивлением, но идеализированный вывод указывает на возможность создания профилей с большими значениями аэродинамического качества K. У применяемых в авиации дозвуковых профилей значения K могут достигать 50 и более.
В. А. Башкин.
Энциклопедия «Авиация». - М.: Большая Российская Энциклопедия. Свищёв Г. Г.. 1998.
